Parametric equation of the lemniscate ∞ :
(Travail d'initiative personnelle encadré)
(Oral de prépa)
En deux mots. Pour résoudre des équadiffs, Python marche bien. Mais dans des petits systèmes (embarqués par exemple (genre robots)), un circuit peut être beaucoup plus efficace ! C'est grâce à de tels circuits que marchaient les premiers ordinateurs, qui pourraient d'ailleurs faire un comeback grâce à leur efficacité très souhaitée en machine learning.
Avant la révolution numérique, les calculs physiques étaient réalisés à la main et mécaniquement (anticythère), puis électroniquement depuis la fin du XIXe (Lord Kelvin et l'intégration mécanique)[1]. Le numérique a fini par les remplacer, pour deux raisons principales : les ordinateurs numériques font des calculs exacts, et peuvent être programmés pour réaliser une variété infinie de tâches, contrairement à l’analogique qui consiste à réaliser des calculs en se basant sur les propriétés fondamentales de la physique qui est régie entre autres par des équations différentielles (loi des noeuds ou lois de fonctionnement).
Cependant, l’analogique a plusieurs avantages qui les rendent particulièrement performants dans les nouvelles technologies actuelles. Les réseaux de neurones nécessitent une puissance de calcul phénoménale, et les avantages de l'analogique tels que la capacité à réaliser de nombreux calculs en parallèle, sans stockage, ont poussé des entreprises comme Aspinity, qui se base sur les travaux initiés par des chercheurs comme Hava T. Siegelmann[2], à se servir de ces anciennes technologies pour les réutiliser dans des applications modernes.
L'analogique, plus physiquement, possède aussi l'avantage de ne pas échantillonner le réel et de réaliser les calculs en se basant sur les propriétés de la physique, ce qui peut faire gagner en temps de calculs et des facteurs de 1000 en termes de coût énergétique lors d'applications usuelles[3], surtout si l'on considère l’impact écologique actuel du numérique.
La résolution d'équations différentielles par méthodes analogiques est dirigée par une méthode clef décrite dans Analog Computing de Prof. Dr. Bernd Ulmann : la méthode d'intégrations successives[4]. En partant d'une équation de la forme x'' + bx' + cx +d = f, on isole x'' = f - bx' - cx - d. On peut alors intégrer successivement pour obtenir les valeurs x' puis x. Les intégrations sont effectuées par un amplificateur linéaire en configuration intégrateur, ou par un intégrateur mécanique.
Grâce à cette méthode, la « Kelvin's feedback technique », on peut résoudre la plupart des équations différentielles linéaires par intégrations successives. On commence traditionnellement par faire un masse−ressort amorti.
Voici un diagramme analytique associé au problème qu'on réalise généralement afin de programmer le calculateur analogique. Dans le cas du TIPE, il sert à schématiser le circuit électrique qui servira à la résolution. Ce diagramme dérangera par ailleurs certainement ceux qui se connaissent en calcul analogique. Il n'y a pas de volonté de rigueur absolue ici, seuls les éléments graphiques simplificateurs ont été retenus.
(Les boites sont scrollables horizontalement)
On cherche à modéliser l'équation ÿ + α·ẏ + β·y = e. On a
donc ÿ = -α·ẏ -β·y + e. Un sommateur permettra de calculer
ÿ en sommant les trois termes. Chaque terme est obtenu en
intégrant successivement ÿ. Chaque intégration successif est
pondéré par une constante : α et β. On note
qu'un inverseur est nécessaire pour retrouver du
-y en sortie de l'intégrateur.
Ce diagramme peut être converti en circuit électrique :
On utilise des ALI en format intégrateurs (avec des résistances en parallèle pour des problèmes d'amplification de la composante continue). On remarque par ailleurs la nécessité d'avoir un inverseur après l'entrée en faisant les calculs.
On note R' les résistances de 1 MΩ. On résonne
en potentiels.
La loi des nœuds en A donne :
$$ i_{1} +i_{2} +i_{3} =i_{c} +i_{R'} $$
On a donc l'équation suivante, qu'on note (1):
$$ \frac{-V_{i}}{R} +\frac{V_{0}}{\beta R} +\frac{V_{x}}{\alpha R} =-C\frac{dV_{x}}{dt} -\frac{V_{x}}{R} $$
La loi des nœuds en B donne :
$$ \frac{V_{x}}{R} =C\frac{dV_{0}}{dt} -\frac{V_{0}}{R} $$
On isole Vx et on substitue dans (1) :
$$ V_{i} = R^{2} C^{2}\frac{d^{2} V_{0}}{dt^{2}} +\left[\frac{RC}{\alpha } +2RC\frac{R}{R'}\right]\frac{dV_{0}}{dt} +\left[\frac{1}{\beta } +\frac{R}{R'}\left(\frac{1}{\alpha } +\frac{R}{R'}\right)\right] V_{0} $$
On considère que R négligeable devant R', ce
qui donne sous forme normalisée :
$$ \frac{d^{2} V_{0}}{dt} +\left(\frac{1}{\alpha RC}\right)\frac{dV_{0}}{dt} +\frac{V_{0}}{\beta ( RC)^{2}} = \frac{V_{i}}{( RC)^{2}} $$
On prend RC = 1 à une puissance de 10 près, ce qui donnera bien
ce que l'on veut. Il suffit de modifier les coeffs pour correspondre à l'équation
modélisée.
On résout classiquement $$ V_{0}(t) = \left( A \cos(\omega t) + B \sin(\omega t) \right) e^{kt} + K $$
Et on identifie :
$$ \omega = \frac{1}{RC} \sqrt{\frac{1}{\beta} - \frac{1}{4\alpha^2}} $$$$ k = -\frac{1}{2\alpha RC} $$$$ A = -V_{i}(t) \beta $$$$ B = \frac{V_{i}(t) \beta k}{\omega} $$$$ K = V_{i}(t) \beta $$
On a alors des paramètres réglables (α, β, C, R) pour différentes grandeurs de la solution de l'équadiff. (k, w, A, B) : $$ \alpha \rightarrow \text{décroissance exponentielle}, \quad \beta \rightarrow \text{amplitude}, \quad C \rightarrow \text{pseudo-période}, \quad R \rightarrow \text{variable libre} $$
On a deux problèmes ici :
Voici le circuit. Entrée et sortie en A1 et A64. Il manque d'ailleurs les alimentations des ALI sur ce circuit simplifié.
Les deux ALI du milieu sont les intégrateurs. Les deux résistances en haut à droite sont les résistance retour. On utilise des boites à décades en pratique pour les faire varier.
En pratique les cables sont trop longs, donc ça fait une jungle.
Je réalise l'aquisition de plusieurs signaux, pour plusieurs valeurs de alpha, beta, C (je préfère ne pas changer beta à cause de la modification de la valeur finale...).
Je réalise un programme python qui les trace :
undefinedOn obtient une liste de sorties :
(Syntaxe : EXYCZ : alpha = X, beta = Y, C = Z*10 nF)
Voici les résultats pour une entrée en échelon pour le pendule-plan puis pour le circuit d'ordre 2 (E81C3 je crois). Les données du pendule-plan ont été prélevées d'une vidéo par un logiciel de pointage.
En superposant les deux courbes :
On voit que le pendule plan ne suit pas exactement l'allure d'un sinus amorti, je pense parce que Tracker ne traque pas super bien, et parce que la balle de ping-pong qui fait office de pendule est trop sensible aux incertitudes à cause de sa masse faible.
Voici un circuit qui résout des équadiffs numériquement, avec Odeint. Je trace également la sortie exacte, calculée précédemment sur un cahier.
undefinedSortie du programme :
On voit bien que Odeint et la solution calculée à la main sont indiscernables. Le circuit, lui, s'éloigne de la sortie attendue. La valeur finale n'est pas toute à fait la même, certainement à cause de l'incertitude sur Beta et Vi. Cependant, sans résoudre l'équation différentielle, on a une bonne allure de la solution.
Il reste désormais à expliquer cet écart, et à le quantifier.
Numérique > Analogique mais ...
Trouver des exemples où il est préférable d'avoir un circuit qui traite les données en direct, sans échantillonnage.
Analyse énergétique aussi ?
Pour tenter de systématiser un peu le processus de création de circuits, on propose par exemple de créer un circuit qui résout une équadiff linéaire d'ordre n, de la forme :
$$ y^{(n)} +a_{n-1}y^{(n-1)} +\ldots +a_{1}y' +a_{0}y =e $$
Voici un script python qui dessine un circuit théorique.
undefined
Il s'agit seulement d'un circuit théorique : il ne prend pas (encore ?) en compte les problèmes d'amplification de la composante continue. Il est en réalité impossible de mettre autant d'intégrateurs en série, surtout au-delà d'un ordre supérieur à 4. Mais il illustre bien la nécessité d'un inverseur à un retour sur deux, et le lien entre les coefficients de l'équation et les résistances pondérées du circuit.
Avant de cerner précisément la problématique et d'acquérir les connaissances précises, j'ai voulu explorer toutes les facettes du domaine, en particulier les méthodes de résolution mécaniques.
À la place d'utiliser des ALI pour intégrer successivement, on peut le faire mécaniquement avec cet intégrateur mécanique. Il faut ensuite assembler plusieurs de ces intégrateurs et ajouter des inverseurs et sommateurs (assez simples normalement) pour créer un circuit mécanique qui résout des équadiffs.
Voici une tentative d'intégration mécanique. J'ai enlevé le support d'écriture afin de comprendre son fonctionnement :
Un moteur permet de fournir une vitesse de rotation constante à la plaque
carrée (je n'avais pas de disque). Plus haut, un module translatable
permet le traçage de la courbe dont l'intégrale est voulue. La vitesse de
rotation de la roue dépend de la position de cette dernière sur le
"disque" en rotation. La distance de son point d’appui avec le centre du
disque,
y, varie dans le temps. Cette distance est contrôlée à la
main en haut à droite. Quand le disque tourne d’un angle infinitésimal dθ,
pendant un intervalle de temps βdτ, l’axe de la roue tourne
d’un angle
y(τ) dθ. Pendant un intervalle de temps
[0, t], l’axe de la roulette tourne donc d’un angle
α ∫ y(τ) β dτ. Le cylindre en bois transmet donc la vitesse
de rotation à une vis sans fin qui permet le traçage de l’intégrale (de 0
à t) : ∫ y(τ) dτ, à un facteur de proportionnalité près.
Pour le dire simplement, plus la roue est éloignée du centre de rotation de la plateforme, plus elle tourne vite. Une relation linéaire entre vitesse et positon une opération de dérivée, et donc d'intégration dans l'autre sens.
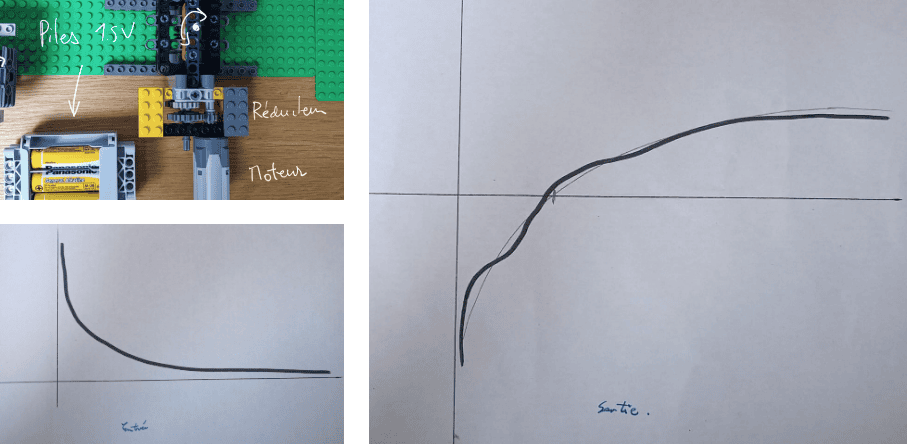
On obtient les résultats suivants :
L'entrée est dessinée à la main en faisant translater le module translatable : la valeur de cette translation donne les y en fonction du temps. Les x sont données par la translation d'une feuille dont la vitesse est donnée par le moteur. Cette vitesse est synchronisée à celle de la translation de la feuille de sortie. Ici, j'ai tenté d'intégrer une courbe en 1/x en essayant de coller le plus possible au graphe que j'ai tracé au préalable.
On voit bien que la sortie correspond grossièrement à du ln(x), même si on observe des erreurs. Ces erreurs sont dues à la transmission de la vitesse de rotation de la roue jusqu'à la roue et vis sans fin. Il y a souvent des accrochages qui créent un retard (ralentissement de la pente), qui est ensuite compensé quand la rotation reprend après le blocage.
On voit bien que l'intégration mécanique n'est pas très optimisée : j'abandonne donc cette piste.